Phase Accumulation
26 Jan 2019Making (sine) waves
Let’s say you need to generate a sine wave, one reason for wanting this will become clear in later posts. The most commonly used method is a phase accumulator.
First you need a counter, I’m using a 32-bit one which can store values between 0 and 4,294,967,295, and let this represents the phase between 0 and 2π.
For each sample you want to generate you convert the phase value into the output, then add a step to move to the next one. Calculating the step size is easy: step = (max accumulator value * frequency) / sample rate .
One nice thing about this method is when you go past the end, normal integer overflow kicks in and wraps the value around. This maintains any fractional part of the phase which ensures the value doesn’t drift.
Now division isn’t great on a microcontroller but as it’s by a constant you can convert it to the reciprocal (e.g. 1/number) and multiply by that. So instead of dividing by 48000, you multiply by 0.00002083333333333333. On the cortex-m4 processor I’m using a divide is between 2 and 12 cycles, where multiply is 1, so it’s a pretty big saving. Also, once you’ve changed it to a multiply you can reorder it and combine the reciprocal with the maximum value, so it’s just one multiply against a constant. The step only changes with frequency, so most of the time you just calculate this and re-use it.
Now you’ve got the current phase, and a way of updating it, you need to convert it to sine. The built-in maths function would be a good place to start, but on some devices it’s not the quickest thing. Looking at the standard library for the compiler I’m using it’s around 30 instructions (depending on what the value is), so can we do better?
Lookup tables
The most common method for doing this in hardware is a big lookup table, that way you don’t even have to worry about converting the phase accumulator value into radians. If you’ve got a 12-bit DAC (Digital to Analog converter), you could just use the top 12 bits of the accumulator as the index and you’re done.
Why only the top 12-bits? Well, the table gets big quickly (212 = 4096, 213 = 8129, 216 = 65536) so while it’s useful to track the phase with higher accuracy there’s no point in using more bits then you need for the output.
However, it’s recommended to use a table 1 to 2 bits larger than your output, as this lets you control the rounding (there’s an example of this in the table near the end of this post). Using a lookup leads to truncation (as you’re throwing away the lower bits of the accumulators’ value), which causes distortion. By using some extra bits, you can choose a closer value e.g. round up to 1 from 0.9 rather than truncating to 0.
Doing this is fine in hardware, as you’ll have dedicated memory for this, but on a micro-controller these tables can take up a lot of your, already limited, memory. If only there was a way of guessing the in-between values accurately, so we didn’t need to store them.
Making things up
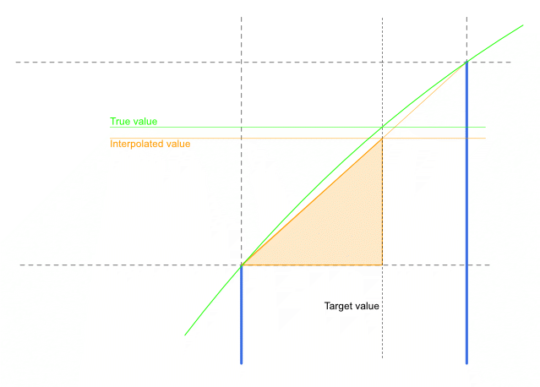
As sine is a continuous function, e.g. the values change in a regular way, if your samples are close enough together a straight line between them is almost the same. The following picture should give you a good idea of what we’re trying to do.
As you can see the orange (interpolated) line is pretty close to the true (green) curve. This example only has 24 samples spread over the whole 2π so is much coarser than you’d use when implementing this, which is quite simple:
# i is the index into the table, from the top bits of the accumulator.
# f is the lower bits of the accumulator,
# converted into a floating point value between 0 and 1.
# Lookup the value of the first sample.
a = lookup[i]
# Get the value on the next sample
b = lookup[i + 1]
# Subtract A from B, to find out how much it changes.
difference = b - a
# Multiply D by the fractional part of the phase accumulators value, and add it to A.
result = (difference * f) + a
To make things simpler you can make the table one item larger then you need and copy the first entry. This way you don’t need to worry about going past the end if you hit the last entry.
You might be wondering how well this works, so I wrote a little Go program to compare the values from calculating sine using double precision floating point against various size lookup tables, both with and without interpolation.
| Table size (bits) | Table size (entries) | Direct | Interpolated | ||||
|---|---|---|---|---|---|---|---|
| Smallest Error | Largest Error | Average Error | Smallest Error | Largest Error | Average Error | ||
| 18 | 262,144 | 0 | 1 | 0.250 | 0 | 1 | 0.250 |
| 17 | 131,072 | 0 | 2 | 0.500 | 0 | 1 | 0.395 |
| 16 | 65,536 | 0 | 4 | 1.000 | 0 | 1 | 0.449 |
| 15 | 32,768 | 0 | 7 | 2.000 | 0 | 1 | 0.474 |
| 14 | 16,384 | 0 | 13 | 4.000 | 0 | 1 | 0.488 |
| 13 | 8,192 | 0 | 26 | 8.000 | 0 | 1 | 0.494 |
| 12 | 4,096 | 0 | 51 | 15.999 | 0 | 2 | 0.497 |
| 11 | 2048 | 0 | 101 | 31.999 | 0 | 2 | 0.500 |
| 10 | 1,024 | 0 | 201 | 63.996 | 0 | 2 | 0.501 |
| 9 | 512 | 0 | 402 | 127.993 | 0 | 2 | 0.534 |
| 8 | 256 | 0 | 804 | 255.984 | 0 | 4 | 1.125 |
| 7 | 128 | 0 | 1607 | 511.969 | 0 | 11 | 4.141 |
As you can see, a 9-bit table with interpolation gives a lower error then a 16-bit one without. If you’re storing each item as a 16-bit value that’s a saving of 127KB.
You can also see the benefits of using the extra bits in a hardware lookup, a 16-bit table has an average error of 1 and a largest of 4, while the 18 bit reduces that to 0.25 and 1.
Obviously, you don’t get this for free. The bit of assembly I ended up writing works out around 15 instructions for the interpolation, still quicker than the math libraries sine function, but not free. On this project it’s worth it to save the memory.